
We can get this into a simpler form by switching to polar coordinates (r and θ), which are defined in terms of Cartesian coordinates as follows: This may not be in the form you’re used to seeing it (this is really Newton’s law of gravity in disguise). The gravitational force, using these would then be: Here, we simply have the gradient in two dimensions. So, the partial derivative with respect to x is then: If we take the partial derivatives of this with respect to both x and y, we get: Here, I’m essentially just using the power rule for derivatives as well as the chain rule. This is now in a form which we can easily take the gradient of. Here, r is the distance between the two masses, which we can express, using the Pythagorean theorem, as: I’m assuming that the situation is in the 2-dimensional xy-plane, but you can equivalently repeat the calculation for 3-dimensions, in which case you’d have r 2=x 2+y 2+z 2. The gravitational potential energy between two masses (M and m) is: Practical Example: Gravitational Force and Potential Energy

The curl is essentially a vector operator that is also defined in terms of partial derivatives. In fact, this also gives us a nice way to check whether a force is conservative or not by taking the curl of the force (we’ll discuss this later). Therefore, we can also say that any conservative force can be written as the gradient of some scalar function. This definition also works mathematically the curl of any conservative force is zero, but so is the curl of the gradient of any scalar function.

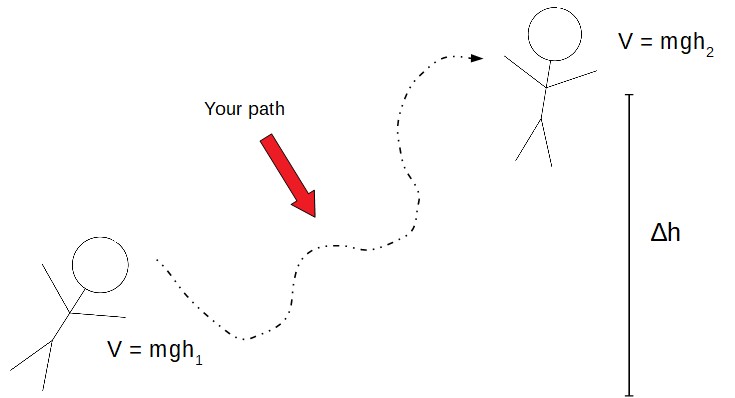
We’ll talk more about path independence later in this article, but essentially, all conservative forces are path independent. In this case, the vector field would be the force and the scalar field would be the potential. Well, this is actually a consequence of a much deeper result in vector calculus a path independent vector field can always be written as the gradient of some scalar field. Now, you may want to ask why exactly can a conservative force be defined in terms of the gradient of a potential? This can be seen, for example, in a gravitational field, but also in the energy states of electrons in an atom (notice also that these are examples of conservative forces, namely the gravitational force and the electrostatic force). Perhaps this property sheds some light to the fact that most objects in nature tend to behave in such a way that their potential is minimized. The (conservative) force due to this potential would then “push” the particle in a direction such that its potential would be the lowest (the direction of greatest decrease).

Physically, we can interpret this by imagining that we place a particle in some potential. Now, since the force is defined as the negative gradient of the potential energy, it always points in the direction in which the potential energy is decreasing the fastest. If we visualize the scalar function (potential energy) as a “hill” with the height describing its value, then the gradient of the potential would be a vector that points in the “steepest” direction along the hill: Here, we have a potential that’s a function of x and y only so that it can be visualized as a “hill”. Geometrically, the gradient of any scalar function represents the direction in which the scalar function is changing the fastest. So, to actually calculate this gradient of the potential, we take partial derivatives of it with respect to each position coordinate and then form a vector (the force) as follows: The potential energy U here is generally a function of position (which in 3D Cartesian coordinates would be U(x,y,z)) and so is the force. Now, a gradient is an operator in vector calculus that acts on a scalar function (the potential in this case) and gives a vector as a result (the force): Mathematically, any conservative force can be expressed through this relationship as F=-∇U. The relationship between a conservative force and potential energy is that a conservative force is defined as the negative gradient of a potential associated with that force.


 0 kommentar(er)
0 kommentar(er)
